This summer I had plenty of time during COVID-19 lockdown and I was looking at SymPy Gamma.

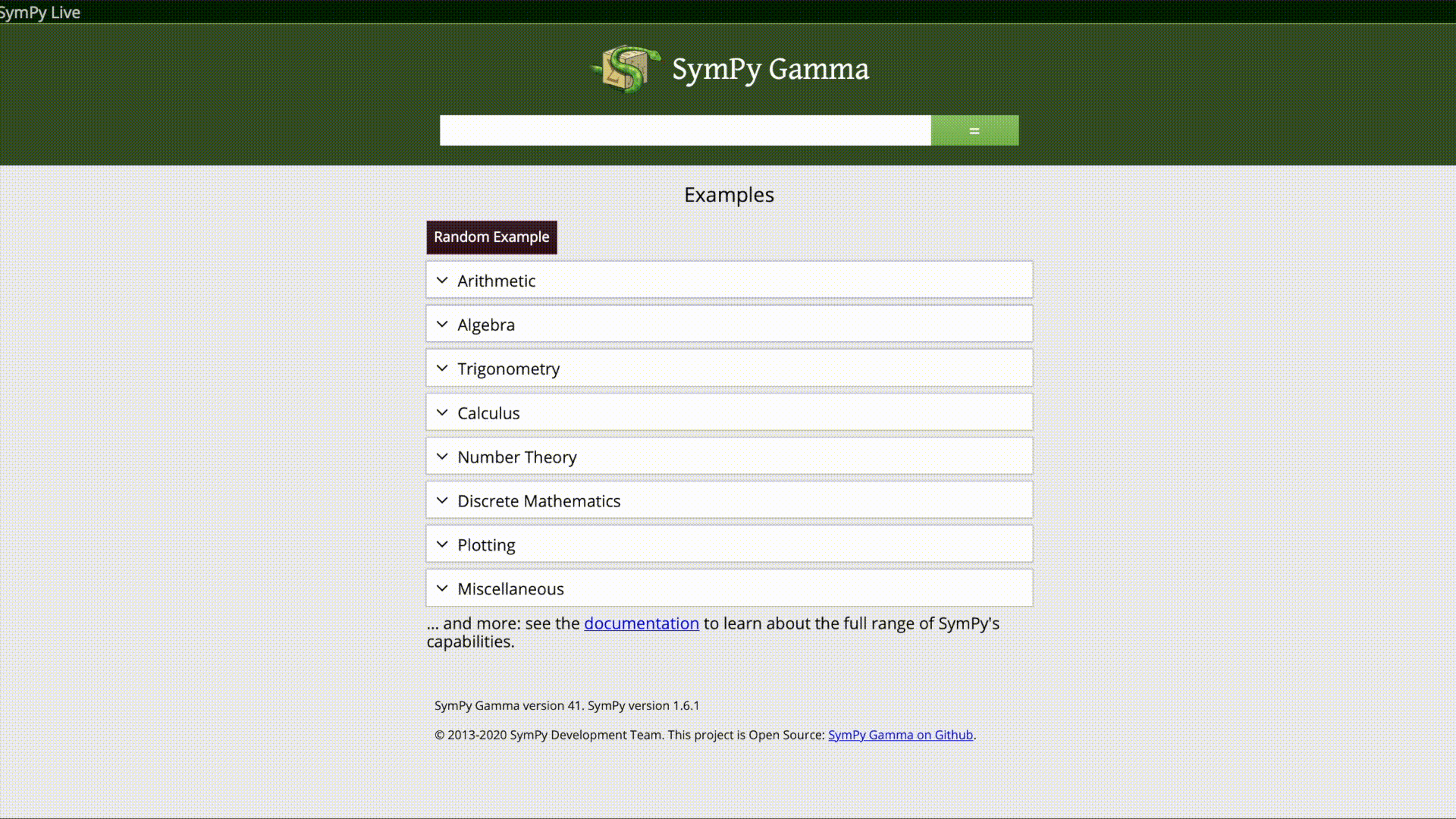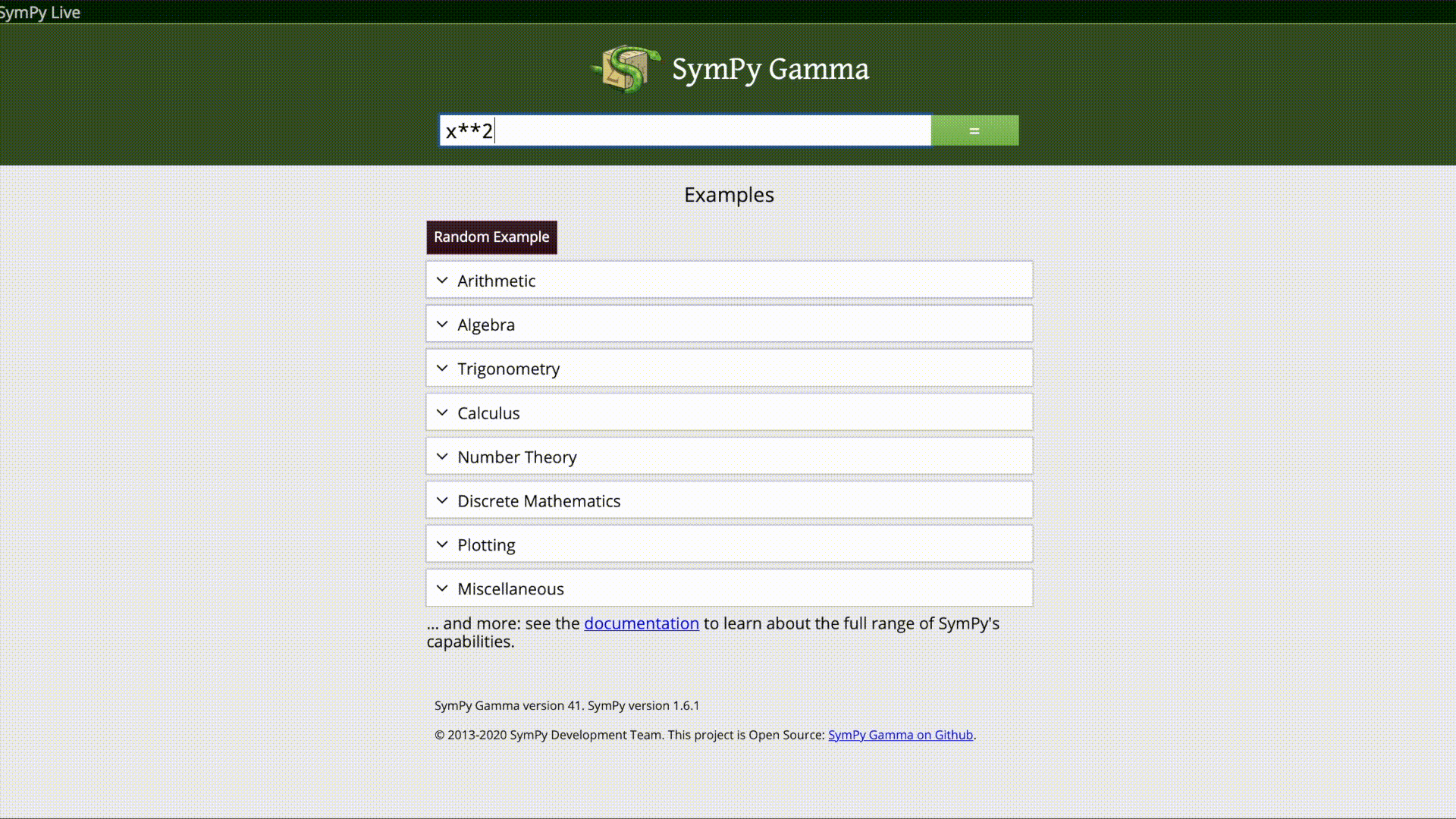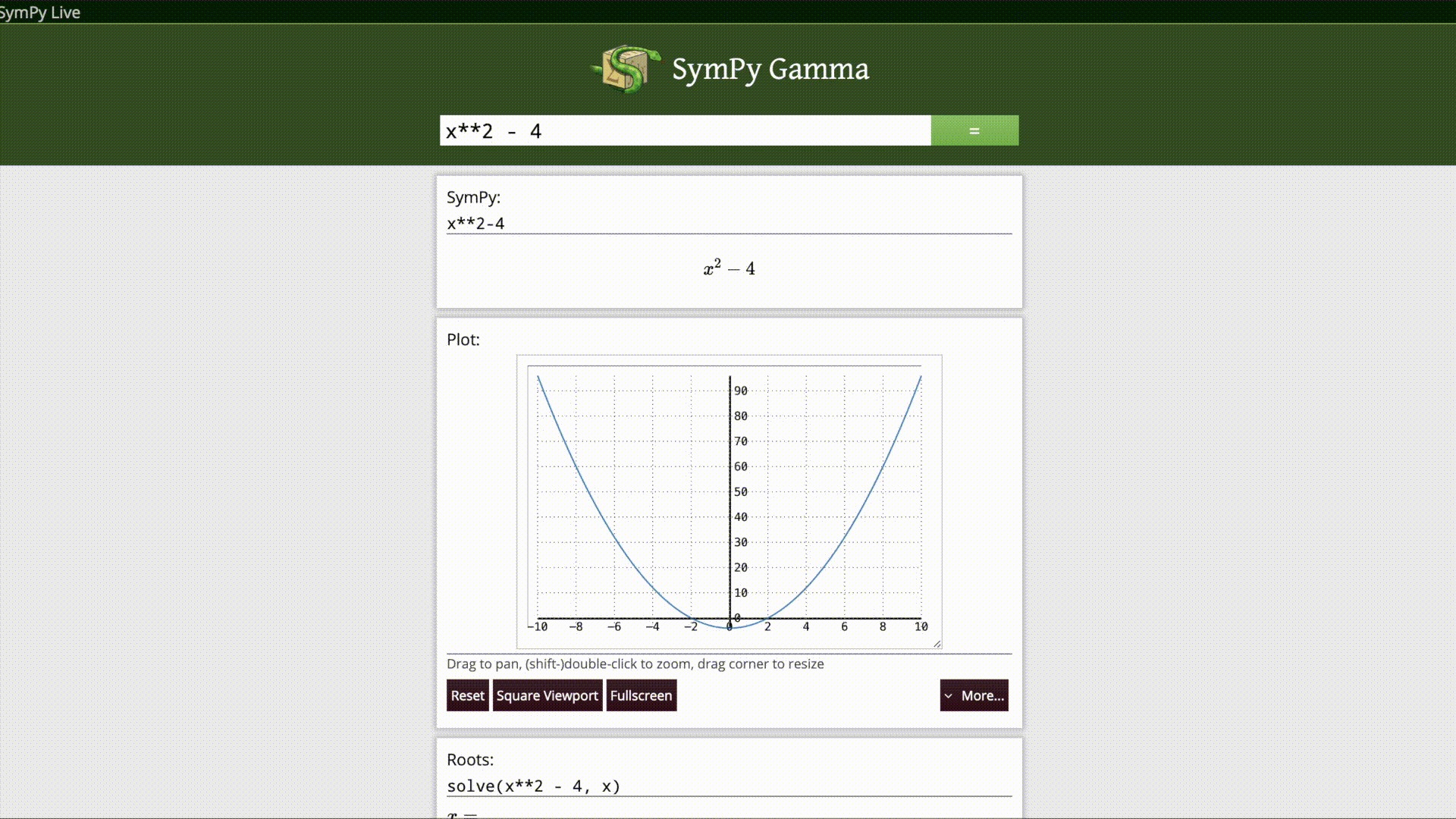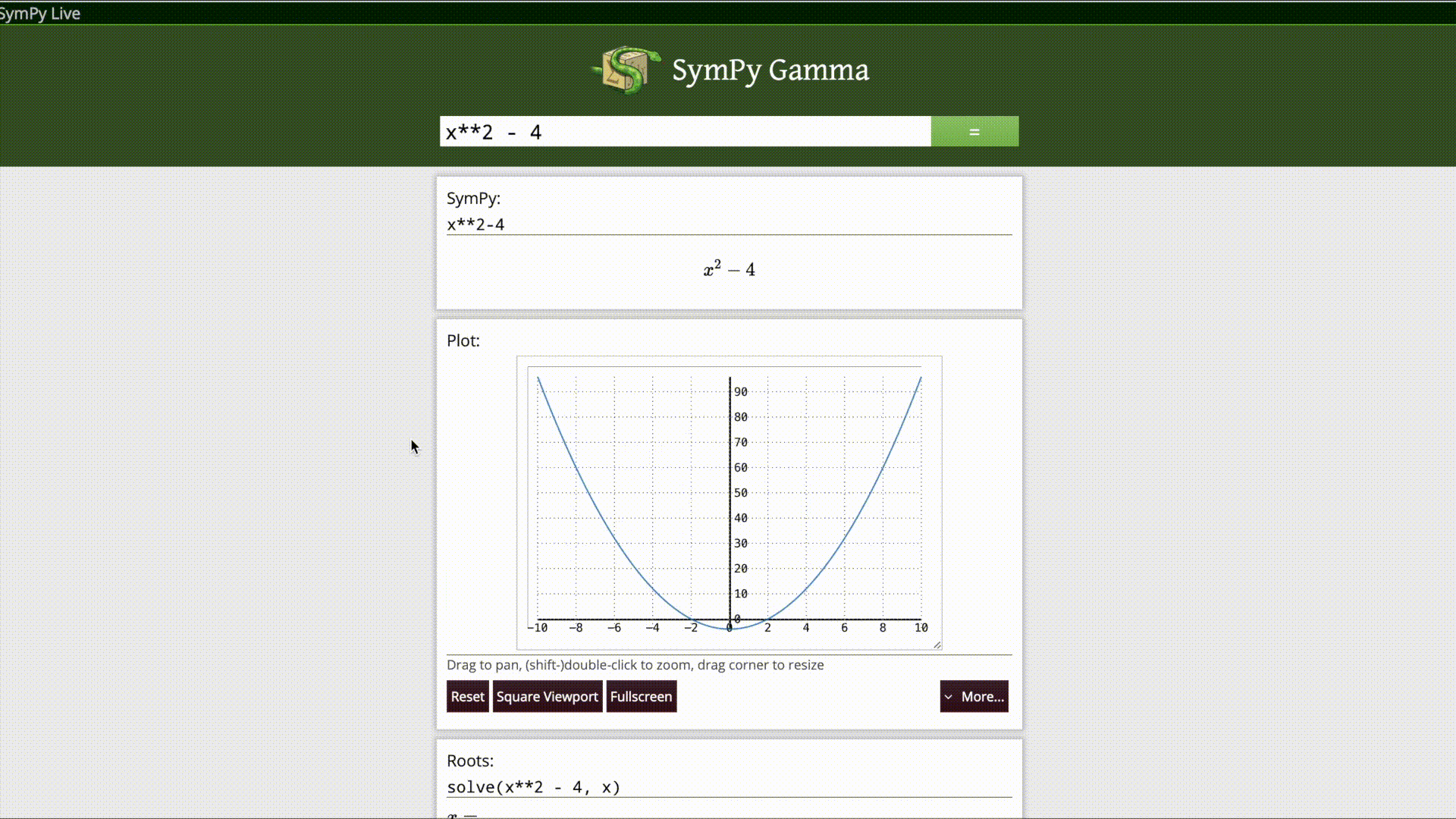
Sympy Gamma

SymPy Gamma is a web application that executes mathematical expressions via natural language input from the user, after parsing them as SymPy expressions it displays the result with additional related computations. It is inspired from the idea of WolframAlpha which is based on the commercial Computer Algebra System named “Mathematica”.

I have always been impressed by it ever since I first found about it. While playing with it during this summer, I realised that it runs on Google App Engine’s Python 2.7 runtime. It is powered by SymPy, an open source computer algebra system.

The Problem

Despite being widely used around the world (about ~14K users everyday, as seen from Google Analytics), there hasn’t been a lot of development in the past 5 years. Due to this the current infrastructure was stuck on Google App Engine’s Python 2 runtime which obviously does not support Python 3.

This also prevented it to use the latest version of SymPy. The SymPy version (~0.7.6) it was using was last updated 6 years ago. This made SymPy Gamma in urgent need for upgradation. At the time of writing this blog, SymPy Gamma is running on Google App Engine’s latest runtime and latest version of SymPy.

Solution and Process

It was a fun project and was interesting to see how Google cloud offering has evolved from Google App Engine to Google Cloud Platform. The old App engine did seem like a minimal cloud offering launched by Google in an attempt to ship something early and quickly. It reminded me of my first cloud project in college (dturmscrap), which I deployed to Google App Engine, back in 2015.

I used Github projects to track the whole project, all the work done for this can be seen here.

$ Git Log

Here is a summary of what was achieved:

• PR 135: Migrating Django to a slightly higher version, this was the first blood just to make sure everything was working. I upgraded it to the latest version of Django that was supported on Python 2 runtime. This also exposed the broken CI, which was fixed in this.

• PR 137: This upgraded the CI infrastructure to use Google Cloud SDK for deployment, the previous method was discontinued.

• PR 140: Upgrading the Database backend to use Cloud NDB instead of the legacy App Engine NDB.

• PR 148: Since we change the database backend, we needed something for testing locally, this was done by using Google Cloud Datastore emulator locally.

• PR 149: The installation and setup of the project was quite a challenge. Installing and keeping track of the versions of a number of application was non-trivial. This Pull request dockerized the project and made the development setup trivial and it all boiled down to just one command.

• PR 152: The login feature was previously implemented using the user API of the Google App Engine’s Python2 runtime, which was not available in Python 3 runtime. We removed the login feature as it was not used by many and was too much effort to setup OAuth for login.

• PR 153: Now was the time to slowly move towards Python 3 by making the code compatible with both 2 and 3. It was achieved via python-modernize.

• PR 154: We then made the migration to Python 3.7 runtime and removed submodules and introduced a requirements.txt for installing dependencies.

• PR 159: The above change made it possible to upgrade SymPy to latest version, which was 1.6 at that time.

• PR 165: The last piece of the puzzle was upgrading Django itself, so we upgraded it to the latest version, which was Django 3.0.8.

Next Steps

• At the time of writing this Google has released the Python 3.8 runtime, it would nice to further upgrade it now.
• The test coverage can be increased.
• The code can be refactored to be more readable and approachable for new contributors.

Thanks to Google for properly documenting the process, which made the transition much easier.

Thanks to NumFocus, without them this project would not have been possible. Also thanks to Ondrej Certik and Aaron Meurer for their advice and support throughout the project.

This report summarizes the work done in my GSoC 2020 project, Implementation of Vector Integration with SymPy. Blog posts with step by step development of the project are available at friyaz.github.io.

About Me

I am Faisal Riyaz and I have completed my third year of B.Tech in Computer Engineering student from Aligarh Muslim University.

Overview

The goal of the project is to add functions and class structure to support the integration of scalar and vector fields over curves, surfaces, and volumes. My mentors were Francesco Bonazzi (Primary) and Divyanshu Thakur.

Work Completed

Here is a list of PRs which were opened during the span of GSoC:

• (Merged) #19472: Adds ParametricRegion class to represent parametrically defined regions.

• (Merged) #19539: Adds ParametricIntegral class to represent integral of scalar or vector field over a parametrically defined region.

• (Merged) #19580: Modified API of ParametricRegion.

• (Merged) #19650: Added support to integrate over objects of geometry module.

• (Merged) #19681: Added ImplicitRegion class to represent implicitly defined regions.

• (Megred) #19807: Implemented the algorithm for rational parametrization of conics.

• (Merged) #20000: Added API of newly added classes to sympy’s documentation.

• (Open) #19883: Allow vector_integrate to handle ImplicitRegion objects.

• (Open) #20021: Add usage examples.

We had an important discussion regarding our initial approach and possible problems on issue #19320

Defining Regions with their parametric equations

The ParametricRegion class is used to represent a parametric region in space.

>>> from sympy.vector import CoordSys3D, ParametricRegion, vector_integrate
>>> from sympy.abc import r, theta, phi, t, x, y, z
>>> from sympy import pi, sin, cos, Eq

>>> C = CoordSys3D('C')

>>> circle = ParametricRegion((4*cos(theta), 4*sin(theta)), (theta, 0, 2*pi))
>>> disc = ParametricRegion((r*cos(theta), r*sin(theta)), (r, 0, 4), (theta, 0, 2*pi))
>>> box = ParametricRegion((x, y, z), (x, 0, 1), (y, -1, 1), (z, 0, 2))
>>> cone = ParametricRegion((r*cos(theta), r*sin(theta), r), (theta, 0, 2*pi), (r, 0, 3))

>>> vector_integrate(1, circle)
8*pi
>>> vector_integrate(C.x*C.x - 8*C.y*C.x, disc)
64*pi
>>> vector_integrate(C.i + C.j, box)
(Integral(1, (x, 0, 1), (y, -1, 1), (z, 0, 2)))*C.i + (Integral(1, (x, 0, 1), (y, -1, 1), (z, 0, 2)))*C.j
>>> _.doit()
4*C.i + 4*C.j
>>> vector_integrate(C.x*C.i - C.z*C.j, cone)
-9*pi

Integration over objects of geometry module

Many regions like circle are commonly encountered in problems of vector calculus. the geometry module of SymPy already had classes for some of these regions. The functionparametric_region_list was added to determine the parametric representation of such classes. vector_integrate can directly integrate objects of Point, Curve, Ellipse, Segment and Polygon class of geometry module.

>>> from sympy.geometry import Point, Segment, Polygon, Segment
>>> s = Segment(Point(4, -1, 9), Point(1, 5, 7))
>>> triangle = Polygon((0, 0), (1, 0), (1, 1))
>>> circle2 = Circle(Point(-2, 3), 6)
>>> vector_integrate(-6, s)
-42
>>> vector_integrate(C.x*C.y, circle2)
-72*pi
>>> vector_integrate(C.y*C.z*C.i + C.x*C.x*C.k, triangle)
-C.z/2

Implictly defined Regions

In many cases, it is difficult to determine the parametric representation of a region. Instead, the region is defined using its implicit equation. To represent implicitly defined regions, we implemented the ImplicitRegion class.

But to integrate over a region, we need to determine its parametric representation. the rationl_parametrization method was added to ImplicitRegion.

>>> from sympy.vector import ImplicitRegion
>>> circle3 = ImplicitRegion((x, y), (x-4)**2 + (y+3)**2 - 16)
>>> parabola = ImplicitRegion((x, y), (y - 1)**2 - 4*(x + 6))
>>> ellipse = ImplicitRegion((x, y), (x**2/4 + y**2/16 - 1))
>>> rect_hyperbola = ImplicitRegion((x, y), x*y - 1)
>>> sphere = ImplicitRegion((x, y, z), Eq(x**2 + y**2 + z**2, 2*x))

>>> circle3.rational_parametrization()
(8*t/(t**2 + 1) + 4, 8*t**2/(t**2 + 1) - 7)
>>> parabola.rational_parametrization()
(-6 + 4/t**2, 1 + 4/t)
>>> rect_hyperbola.rational_parametrization(t)
(-1 + (t + 1)/t, t)
>>> ellipse.rational_parametrization()
(t/(2*(t**2/16 + 1/4)), t**2/(2*(t**2/16 + 1/4)) - 4)
>>> sphere.rational_parametrization()
(2/(s**2 + t**2 + 1), 2*s/(s**2 + t**2 + 1), 2*t/(s**2 + t**2 + 1))

After PR #19883 gets merged, vector_integrate can directly work upon ImplicitRegion objects.

Future Work

• In vector calculus, many regions cannot be defined using a single implicit equation. Instead, inequality or a combination of the implicit equation and conditional equations is required. For Example, a disc can only be represented using an inequality ImplicitRegion(x**2 + y**2 < 9) and a semicircle can be represented as ImplicitRegion(x**2 + y**2 -4) & (y < 0)). Support for such implicit regions needs to be added.

• The parametrization obtained using the rational_parametrization method in most cases is a large expression. SymPy’s Integral is unable to work over such expressions. It takes too long and often does not returns a result. We need to either simplify the parametric equations obtained or fix Integral to handle them.

• Adding the support to plot objects of ParamRegion and ImplicitRegion

Conclusion

This summer has been a great learning experience. Writing a functionality, testing, debugging it has given me good experience in test-driven development. I think I realized many of the goals that I described in my proposal, though there were some major differences in the plan and actual implementation. Personally, I hoped I could have done better. I could not work much on the project during the last phase due to the start of the academic year.

I would like to thank Francesco for his valuable suggestions and being readily available for discussions. He was always very friendly and helpful. I would love to work more with him. S.Y Lee also provided useful suggestions.

Special thanks to Johann Mitteramskogler, Professor Sonia Perez Diaz, and Professor Sonia L.Rueda. They personally helped me in finding the algorithm for determining the rational parametrization of conics.

SymPy is an amazing project with a great community. I would mostly stick around after the GSoC period as well and continue contributing to SymPy, hopefully, exploring the other modules as well.

This report summarises the work I have done during GSoC 2020 for SymPy. The links to the PRs are in chronological order. For following the progress made during GSoC, see my blog for the weekly posts.

About Me

I am Sachin Agarwal, a third-year undergraduate student majoring in Computer Science and Engineering from the Indian Institute of Information Technology, Guwahati.

Project Synopsis

My project involved fixing and amending functions related to series expansions and limit evaluation. For further information, my proposal for the project can be referred.

Pull Requests

This section describes the actual work done during the coding period in terms of merged PRs.

Phase 1

• #19292 : This PR added a condition to limitinf method of gruntz.py resolving incorrect limit evaluations.

• #19297 : This PR replaced xreplace() with subs() in rewrite method of gruntz.py resolving incorrect limit evaluations.

• #19369 : This PR fixed _eval_nseries method of mul.py.

• #19432 : This PR added a functionality to the doit method of limits.py which uses is_meromorphic for limit evaluations.

• #19461 : This PR corrected the _eval_as_leading_term method of tan and sec functions.

• #19508 : This PR fixed _eval_nseries method of power.py.

• #19515 : This PR added _eval_rewrite_as_factorial and _eval_rewrite_as_gamma methods to class subfactorial.

Phase 2

• #19555 : This PR added cdir parameter to handle series expansions on branch cuts.

• #19646 : This PR rectified the mrv method of gruntz.py and cancel method of polytools.py resolving RecursionError and Timeout in limit evaluations.

• #19680 : This PR added is_Pow heuristic to limits.py to improve the limit evaluations of Pow objects.

• #19697 : This PR rectified _eval_rewrite_as_tractable method of class erf.

• #19716 : This PR added _singularities to LambertW function.

• #18696 : This PR fixed errors in assumptions when rewriting RisingFactorial / FallingFactorial as gamma or factorial.

Phase 3

• #19741 : This PR reduced symbolic multiples of pi in trigonometric functions.

• #19916 : This PR added _eval_nseries method to sin and cos.

• #19963 : This PR added _eval_is_meromorphic method to the class BesselBase.

• #18656 : This PR added Raabe's Test to the concrete module.

• #19990 : This PR added _eval_is_meromorphic and _eval_aseries methods to class lowergamma, _eval_is_meromorphic and _eval_rewrite_as_tractable methods to class uppergamma and rectified the eval method of class besselk.

• #20002 : This PR fixed _eval_nseries method of log.

Miscellaneous Work

This section contains some of my PRs related to miscellaneous issues.

• #19447 : This PR added some required testcases to test_limits.py.

• #19537 : This PR fixed a minor performance issue.

• #19604 : This PR fixed AttributeError in limit evaluation.

Reviewed Work

This section contains some of the PRs which were reviewed by me.

• #19546
• #19660
• #19730
• #19737
• #19743
• #19771
• #19805
• #19824
• #19876
• #19922
• #19974

Issues Opened

This section contains some of the issues which were opened by me.

• #19670 : Poly(E**100000000) is slow to create.
• #19752 : gammasimp can be improved for integer variables.

Examples

This section describes the bugs fixed and the new features added during GSoC.

Fixed Limit Evaluations

>>> from sympy import limit, limit_seq

>>> n = Symbol('n', positive=True, integer=True)
>>> limit(factorial(n + 1)**(1/(n + 1)) - factorial(n)**(1/n), n, oo)
exp(-1)  # Previously produced 0

>>> n = Symbol('n', positive=True, integer=True)
>>> limit(factorial(n)/sqrt(n)*(exp(1)/n)**n, n, oo)
sqrt(2)*sqrt(pi)  # Previously produced 0 

>>> n = Symbol('n', positive=True, integer=True)
>>> limit(n/(factorial(n)**(1/n)), n, oo)
exp(1)  # Previously produced oo 

>>> limit(log(exp(3*x) + x)/log(exp(x) + x**100), x, oo)
3  # Previously produced 9

>>> limit((2*exp(3*x)/(exp(2*x) + 1))**(1/x), x, oo)
exp(1)  # Previously produced exp(7/3)

>>> limit(sin(x)**15, x, 0, '-')
0  # Previously it hanged

>>> limit(1/x, x, 0, dir="+-")
zoo  # Previously raised ValueError

>>> limit(gamma(x)/(gamma(x - 1)*gamma(x + 2)), x, 0)
-1  # Previously it was returned unevaluated

>>> e = (x/2) * (-2*x**3 - 2*(x**3 - 1) * x**2 * digamma(x**3 + 1) + 2*(x**3 - 1) * x**2 * digamma(x**3 + x + 1) + x + 3)
>>> limit(e, x, oo)
1/3  # Previously produced 5/6

>>> a, b, c, x = symbols('a b c x', positive=True)
>>> limit((a + 1)*x - sqrt((a + 1)**2*x**2 + b*x + c), x, oo)
-b/(2*a + 2)  # Previously produced nan

>>> limit_seq(subfactorial(n)/factorial(n), n)
1/e  # Previously produced 0

>>> limit(x**(2**x*3**(-x)), x, oo)
1  # Previously raised AttributeError

>>> limit(n**(Rational(1, 1e9) - 1), n, oo)
0  # Previously it hanged

>>> limit((1/(log(x)**log(x)))**(1/x), x, oo)
1  # Previously raised RecursionError

>>> e = (2**x*(2 + 2**(-x)*(-2*2**x + x + 2))/(x + 1))**(x + 1)
>>> limit(e, x, oo)
exp(1)  # Previously raised RecursionError

>>> e = (log(x, 2)**7 + 10*x*factorial(x) + 5**x) / (factorial(x + 1) + 3*factorial(x) + 10**x)
>>> limit(e, x, oo)
10  # Previously raised RecursionError

>>> limit((x**2000 - (x + 1)**2000) / x**1999, x, oo)
-2000  # Previously it hanged 

>>> limit(((x**(x + 1) + (x + 1)**x) / x**(x + 1))**x, x, oo)
exp(exp(1))  # Previously raised RecursionError

>>> limit(Abs(log(x)/x**3), x, oo)
0  # Previously it was returned unevaluted

>>> limit(x*(Abs(log(x)/x**3)/Abs(log(x + 1)/(x + 1)**3) - 1), x, oo)
3  # Previously raised RecursionError 

>>> limit((1 - S(1)/2*x)**(3*x), x, oo)
zoo  # Previously produced 0

>>> d, t = symbols('d t', positive=True)
>>> limit(erf(1 - t/d), t, oo)
-1  # Previously produced 1

>>> s, x = symbols('s x', real=True)
>>> limit(erf(s*x)/erf(s), s, 0)
x  # Previously produced 1

>>> limit(erfc(log(1/x)), x, oo)
2  # Previously produced 0

>>> limit(erf(sqrt(x)-x), x, oo)
-1  # Previously produced 1

>>> a, b = symbols('a b', positive=True)
>>> limit(LambertW(a), a, b) 
LambertW(b)  # Previously produced b

>>> limit(uppergamma(n, 1) / gamma(n), n, oo)
1  # Previously produced 0

>>> limit(besselk(0, x), x, oo)
0  # Previously produced besselk(0, oo)

Rewrote Mul._eval_nseries()

>>> e = (exp(x) - 1)/x
>>> e.nseries(x, 0, 3)
1 + x/2 + x**2/6 + O(x**3)  # Previously produced 1 + x/2 + O(x**2, x)

>>> e = (2/x + 3/x**2)/(1/x + 1/x**2)
>>> e.nseries(x, n=3)
3 - x + x**2 + O(x**3)  # Previously produced 3 + O(x)

Rewrote Pow._eval_nseries()

>>> e = (x**2 + x + 1) / (x**3 + x**2)
>>> series(e, x, oo)
x**(-5) - 1/x**4 + x**(-3) + 1/x + O(x**(-6), (x, oo))  
# Previously produced x**(-5) + x**(-3) + 1/x + O(x**(-6), (x, oo))

>>> e = (1 - 1/(x/2 - 1/(2*x))**4)**(S(1)/8)
>>> e.series(x, 0, n=17)
1 - 2*x**4 - 8*x**6 - 34*x**8 - 152*x**10 - 714*x**12 - 3472*x**14 - 17318*x**16 + O(x**17)  
# Previously produced 1 - 2*x**4 - 8*x**6 - 34*x**8 - 24*x**10 + 118*x**12 - 672*x**14 - 686*x**16 + O(x**17) 

Added Series Expansions and Limit evaluations on Branch-Cuts

>>> asin(I*x + I*x**3 + 2)._eval_nseries(x, 3, None, 1)
-asin(2) + pi - sqrt(3)*x/3 + sqrt(3)*I*x**2/9 + O(x**3)

>>> limit(log(I*x - 1), x, 0, '-')
-I*pi

Rectified ff._eval_rewrite_as_gamma() and rf._eval_rewrite_as_gamma()

>>> n = symbols('n', integer=True)
>>> combsimp(RisingFactorial(-10, n))
3628800*(-1)**n/factorial(10 - n)  # Previously produced 0

>>> ff(5, y).rewrite(gamma)
120/Gamma(6 - y)  # Previously produced 0

Added Raabe’s Test

>>> Sum(factorial(n)/factorial(n + 2), (n, 1, oo)).is_convergent()
True  # Previously raised NotImplementedError

>>> Sum((-n + (n**3 + 1)**(S(1)/3))/log(n), (n, 1, oo)).is_convergent()
True  # Previously raised NotImplementedError

Rewrote log._eval_nseries()

>>> f = log(x/(1 - x))
>>> f.series(x, 0.491, n=1).removeO()
-0.0360038887560022  # Previously raised ValueError

Future Work

• Refactoring high level functions like series, nseries, lseries and aseries.
• Add _eval_is_meromorphic method or _singularities to as many special functions as possible.
• Work can be done to resolve the issues opened by me (listed above).

Conclusion

This summer has been a great learning experience and has helped me get a good exposure of test-driven development. I plan to continue contributing to SymPy and will also try to help the new contributors. I am grateful to my mentors, Kalevi Suominen and Sartaj Singh for reviewing my work, giving me valuable suggestions, and being readily available for discussions.

Key highlights of this week’s work are:

• Fixed _eval_nseries() of log

  • This was a long pending issue. It was necessary to refactor the _eval_nseries method of log to fix some minor issues.

This marks the end of Phase-3 of the program. Finally, this brings us to the end of Google Summer of Code and I am really thankful to the SymPy Community and my mentor Kalevi Suominen for always helping and supporting me.

GSoC 2020 Report Smit Lunagariya: Improving and Extending stats module

Key highlights of this week’s work are:

• Implemented Raabe’s Test

  • This was a long pending issue. Raabe's Test helps to determine the convergence of a series. It has been added to the concrete module to handle those cases when the ratio test becomes inconclusive.
    
    

• Fixed limit evaluations related to lowergamma, uppergamma and besselk function

  • We added _eval_is_meromorphic method to class lowergamma and uppergamma so that some of the limits involving lowergamma and uppergamma functions get evaluated using the meromorphic check already present in the limit codebase. Now, to make lowergamma and uppergamma functions tractable for limit evaluations, _eval_aseries method was added to lowergamma and _eval_rewrite_as_tractable to uppergamma.

    Finally, we also rectified the eval method of class besselk, so that besselk(nu, oo) automatically evaluates to 0.

This is the final blog of the official program highlighting the final week. Some of the key discussions were:

Key highlights of this week’s work are:

• Added _eval_is_meromorphic() to bessel function

  • We added the _eval_is_meromorphic method to the class BesselBase so that some of the limits involving bessel functions get evaluated using the meromorphic check already present in the limit codebase.

This blog describes the 11th week of the program. Some of the key highlights of this week are:

Key highlights of this week’s work are:

• Fixed periodicity of trigonometric function

  • This was a long pending issue. The _peeloff_pi method of sin had to be rectified to reduce the symbolic multiples of pi in trigonometric functions. As a result of this fix, now sin(2*n*pi + 4) automatically evaluates to sin(4), when n is an integer.
    
    

• Fixed limit evaluations related to trigonometric functions

  • In this PR, we added _eval_nseries method to both sin and cos to make the limit evaluations more robust when it comes to trigonometric functions. We also added a piece of code to cos.eval method so that the limit of cos(m*x), where m is non-zero, and x tends to oo evaluates to AccumBounds(-1, 1).

This blogs describes the 10th week of the program. Some of the highlights of this week are:

This blogs describes the week 9, the beginning week of the final phase. This week, I continued to work on the extension of Compound Distributions as well as completing the Matrix Distributions. Some of the highlights of this week are:

This blog provides the brief description of last week of the second Phase i.e. week 8. Some of the key highlights of this week are:

This week, I spent most of my time reading about algorithms to parametrize algebraic curves and surfaces.

Parametrization of algebraic curves and surfaces

In many cases, it is easiar to define a region using an implicit equation over its parametric form. For example, a sphere can be defined with the implict eqution x² + y² + z² = 4. Its parametric equation although easy to determine are tedious to write.

To integrate over implicitly defined regions, it is necessary to determine its parametric representation. I found the report on conversion methods between parametric and implicit curves from Christopher M. Hoffmann very useful. It lists several algorithms for curves and surfaces of different nature.

Every plane parametric curve can be expressed as an implicit curve. Some, but not all implicit curves can be expressed as parametric curves. Similarly, we can state of algebraic surfaces. Every plane parametric surface can be expressed as an implicit surface. Some, but not all implicit surfaces can be expressed as parametric surfaces.

Conic sections

One of the algorithm to parametrize conics is given below:

1. Fix a point p on the conic. Consider the pencil of lines through p. Formulate the line equations.
2. Substitute for y in the conic equation, solve for x(t).
3. Use the fine equations to determine y(t).

The difficult part is to find a point on the conic. For the first implementation, I just iterated over a few points and selected the point which satisfied the equation. I need to implement an algorithm that can find a point on the curve.

The parametric equations determined by the algoithm are large and complex expressions. The vector_integrate function in most cases is taking too much time to calculate the integral. I tried fixing this using simplification functions in SymPy like trigsimp and expand_trig. The problem still persist.

>>> ellipse = ImplicitRegion(x**2/4 + y**2/16 - 1, x, y)
>>> parametric_region_list(ellipse)
[ParametricRegion((8*tan(theta)/(tan(theta)**2 + 4), -4 + 8*tan(theta)**2/(tan(theta)**2 + 4)), (theta, 0, pi))]
>>> vector_integrate(2, ellipse)
### It gets stuck

The algorithm does not work for curves of higher algebraic degree like cubics.

Monoids

A monoid is an algebraic curve of degree n that has a point of multiplicity n -1. All conics and singular cubics are monoids. Parametrizing a monoid is easy if the special point is known.

To parametrize a monoid, we need to determine a singular point of n - 1 multiplicity. The singular points are those points on the curve where both partial derivatives vanish. A singular point (xo, yo) of a Curve C is said to be of multiplicity n if all the partial derivatives off to order n - 1 vanish there. This paper describes an algorithm to calculate such a point but the algorithm is not trivial.

Next week’s goal

My goal is to complete the work on parametrizing conics. If I can find a simple algorithm to determine the singular point of the required multiplicity, I will start working on it.

My goal for this week was to add support of integration over objects of geometry module.

Integrating over objects of geometry module

In my GSoC proposal, I mentioned implementing classes to represent commonly used regions. It will allow a user to easily define regions without bothering about its parametric representation. SymPy’s geometry module has classes to represent commonly used geometric entities like line, circle, and parabola. Francesco told me it would be better to add support to use these classes instead. The integral takes place over the boundary of the geometric entity, not over the area or volume enclosed.

My first approach was to add a function parametric_region to the classes of geometry module. Francesco suggested not to modify the geometry module as this would make it dependent on vector module. We decided to implement a function parametric_region to return a ParametricRegion of objects of geometry module.

I learned about the singledispatch decorater of python. It is used to create overloaded functions.
Polygons cannot be represented as a single ParametricRegion object. Each side of a polygon has its separate parametric representation. To resolve this, we decided to return a list of ParametricRegion objects.

My next step was to modify vector_integrate to support objects of geometry module. This was easy and involved calling the parametric_region_list function and integrating each ParametricRegion object.

The PR for the work has been merged. Note that we still do not have any way to create regions like disc and cone without their parametric representation. To support such regions, I think we need to add new classes to the geometry module.

Next week’s goal

I plan to work on implementing a class to represent implicitly defined regions.

The first phase of GSoC is over. We can now integrate the scalar or vector field over a parametrically defined region.

The PR for ParametricIntegral class has been merged. In my last post, I mentioned about a weird error. It turns out that I was importing pi as a symbol instead of as a number. Due to this, the expressions were returned unevaluated causing tests to fail.

The route ahead

I had a detailed discussion with Francesco about the route ahead. My plan has drifted from my proposal because we have decided not to implement new classes for special regions like circles and spheres. The geometry module already has classes to represent some of these regions. We have decided to use these classes.

Francesco reminded me that we have to complete the documentation of these changes. I was planning to complete the documentation in the last phase. But I will try completing it soon as I may forget some details.

We also discussed adding support to perform integral transformation using Stoke’s and Green’s theorem. In many cases, such transformation can be useful but adding them may be outside the scope of this project.

I have convinced Francesco on adding classes to represent implicitly defined regions. It might be the most difficult part of the project but hopefully, it will be useful to SymPy users.

Next week’s goal

My next week’s goal is to make a PR for adding suppor to integrate over objects of the geometry module.

Key highlights of this week’s work are:

• Fixed incorrect limit evaluation related to LambertW function

  • This was a minor bug fix. We added the _singularities feature to the LambertW function so that its limit gets evaluated using the meromorphic check already present in the limit codebase.
    
    

• Fixed errors in assumptions when rewriting RisingFactorial / FallingFactorial as gamma or factorial

  • This was a long pending issue. The rewrite to gamma or factorial methods of RisingFactorial and FallingFactorial did not handle all the possible cases, which caused errors in some evaluations. Thus, we decided to come up with a proper rewrite using Piecewise which accordingly returned the correct rewrite depending on the assumptions on the variables. Handling such rewrites using Piecewise is never easy, and thus there were a lot of failing testcases. After spending a lot of time debugging and fixing each failing testcase, we were finally able to merge this.

This marks the end of Phase-2 of the program. I learnt a lot during these two months and gained many important things from my mentors.

This blog describes the 7th week of the program and the 3rd week of Phase 2. Some of the key highlights on the discussions and the implementations during this week are:

Key highlights of this week’s work are:

• Improved the limit evaluations of Power objects

  • This PR improves the limit evaluations of Power objects. We first check if the limit expression is a Power object and then accordingly evaluate the limit depending on different cases. First of all, we express b**e in the form of exp(e*log(b)). After this, we check if e*log(b) is meromorphic and accordingly evaluate the final result. This check helps us to handle the trivial cases in the beginning itself.

    Now, if e*log(b) is not meromorphic, then we separately evaluate the limit of the base and the exponent. This helps us to determine the indeterminant form of the limit expression if present. As we know, there are 3 indeterminate forms corresponding to power objects: 0**0, oo**0, and 1**oo, which need to be handled carefully. If there is no indeterminate form present, then no further evaluations are required. Otherwise, we handle all the three cases separately and correctly evaluate the final result.

    We also added some code to improve the evaluation of limits having Abs() expressions. For every Abs() term present in the limit expression, we replace it simply by its argument or the negative of its argument, depending on whether the value of the limit of the argument is greater than zero or less than zero for the given limit variable.

    Finally, we were able to merge this after resolving some failing testcases.
    
    

• Fixed limit evaluations involving error functions

  • The incorrect limit evaluations of error functions were mainly because the tractable rewrite was wrong and did not handle all the possible cases. For a proper rewrite, it was required that the limit variable be passed to the corresponding rewrite method. This is because, to define a correct rewrite we had to evaluate the limit of the argument of the error function, for the passed limit variable. Thus, we added a default argument limitvar to all the tractable rewrite methods and resolved this issue. While debugging, we also noticed that the _eval_as_leading_term method of error function was wrong, hence it was also fixed.

    Finally, we were able to merge this after resolving some failing testcases.

This blog describes the 6th week of the official program and the 2nd week of Phase 2. By the end of this week, Compound Distributions framework is ready as targeted and I would now focus on the Joint Distributions in the upcoming weeks of this Phase.

Key highlights of this week’s work are:

• Fixed RecursionError and Timeout in limit evaluations

  • The Recursion Errors in limit evaluations were mainly due to the fact that the indeterminant form of 1**oo was not handled accurately in the mrv() function of the Gruntz algorithm. So, some minor changes were required to fix those.

    The major issue was to handle those cases which were timing out. On deep digging, we identified that the cancel() function of polytools.py was the reason. Thus, we decided to completely transform the cancel() function to speed up its algorithm. Now after this major modification, many testcases were failing as the cancel() function plays an important role in simplifying evaluations and is thus used at many places across the codebase. Therefore, a lot of time was spent in debugging and rectifying these testcases.

    Finally we were able to merge this, enhancing the limit evaluation capabilities of SymPy.

This blogs describes the week 5, the beginning week of the Phase 2. Phase 2 will be mostly focused on Compound Distributions which were stalled from 2018, and additions to Joint Distributions.

I spent this week working on the implementation of the ParametricIntegral class.

Modifying API of ParametricRegion

When I was writing the test cases, I realized that the API of the ParametricRegion could be improved. Instead of passing limits as a dictionary, tuples can be used. So I modified the API of the ParametricRegion class. The new API is closer to the API of the integral class and more intuitive. I made a separate PR for this change to make it easy for reviewers.

Example of the new API:

ParametricRegion( ( x+y, x*y ), (x, 0, 2), (y, 0, 2))

Handling scalar fields with no base scalars

As discussed in previous posts, we decided to not associate a coordinate system with the parametric region. Instead, we assume that the parametricregion is defined in the coordinate system of the field of which the integral is being calculated. We calculate the position vector and normal vector of the parametric region using the base scalars and vectors of the fields. This works fine for most cases. But when the field does not contain any base scalar or vector in its expression, we cannot extract the coordinate system from the field.

ParametricIntegral(150, circle)
# We cannot determine the coordinate system from the field. 
# To calculate the line integral, we need to find the derivative of the position vector.
# This is not possible until we know the base vector of the field

To handle this situation, I assign a coordinate system C to the region. This does not affect the result in any way as the result is independent of it. It just allows the existing algorithm to work in this case.

Separate class for vector and scalar fields

Francesco suggested making separate classes based on the nature of the field: vector and scalar. I am open to this idea. But I think it will be more easy and intuitive for the users if they can use the same class to calculate the integral. I do not think they are different enough from a user’s perspective to have a separate interface.

Maybe we can have a function vectorintegrate which returns the object of ParametricVectorIntegral or ParametricScalarIntegral depending on the nature of the field. This can work for other types of integrals too. Suppose we implement a class ImplicitIntegral to calculate the integral over an implicit region. The vectorintegrate function can then return an object of ImplicitIntegral object by identifying the region is defined implicitly. I think this will be great. I will have more discussion with Francesco on this aspect.

Topological sort of parameters

When evaluating double integral, the result some times depend upon the order in which the integral is evaluated. If the bounds of one parameter u depend on another parameter v, we should integrate first with respect to u and then v.

For example, consider the problem of evaluating the area of the triangle.

T = ParametricRegion((x, y), (x, 0, 2), (y, 10 - 5*x))

The area of the triangle is 10 units and should be independent of the order parameters are specified at the time of object initialization. But the double integral depends on the order of integration.

>>> integrate(1, (x, 0, 2), (y, 10 - 5*x))
20 - 10*x
>>> integrate(1, (y, 0, 10 - 5*x), (x, 0, 2))
10

So parameters must be passed to integrate in the correct order. To overcome this issue, we topologically sort the parameters. SymPy already had a function to perform topologically sort in its utilities module. I implemented a function that generates the graph and passes it to the topological_sort function. This made my work easy.

Long computation time of Integrals

Some integrals are taking too long to compute. When base scalars in the field are replaced by their parametric equivalents, the expression of the field becomes large. Further, the integrand is the dot product of the field with a vector or product of the field and the magnitude of the vector. The integrate function takes about 20-30 seconds to calculate the integral. I think this behavior is due to the expression of integrand growing structurally despite it being simple.

For example,

>>>solidsphere = ParametricRegion((r*sin(phi)*cos(theta), r*sin(phi)*sin(theta), r*cos(phi)),\
                                (r, 0, 2), (theta, 0, 2*pi), (phi, 0, pi))
>>> ParametricIntegral(C.x**2 + C.y**2, solidsphere)

In this case, the parametric field when replaced with parametersr become r**2*sin(phi)**2*sin(theta)**2 + r**2*sin(phi)**2*cos(theta)**2 although it can be easily simplified to r**2*sin(phi).

SymPy has a function called simplify. simplify attempts to apply various methods to simplify an expression. When the integrand is simplified using it before passing to integrate, the result is returned almost immediately. Francesco rightly pointed out that simplify is computationally expensive and we can try to some specific simplification. I will look into it.

Failing test cases

Some test cases are failing because of integrate function returning results in different forms. The results are mathematically equivalent but different in terms of structure. I found this strange. I do not think this has to do with hashing. I still have not figured out this problem.

Next week’s goal

Hopefully, I will complete the work on the ParamatricIntegral and get it merged. We can then start discussing about representing implicit regions.

Part of this week was spent in getting the PR for ParametricRegion merged. I made some fixes to get the failing tests to pass. I also added the docstring.

ParametricIntegral

I started working on the ParametricIntegral class. ParametricIntegral class returns the integral of a scalar or vector field over a region defined parametrically. It should be able to calculate line, surface, or volume integral depending on the nature of the parametric region. To identify the nature of the region, the dimensions property needs to be added in the ParametricRegion class.

I started with writing the test cases to avoid my previous mistake of working on the implementation before deciding the API. The API of the ParametricIntegral class:

ParametricIntegral(field, parametricregion)

Some examples:

>>> curve = ParametricRegion((3*t - 2, t + 1), {t: (1, 2)})
>>> ParametricIntegral(C.x, curve)
5*sqrt(10)/2
>>> semisphere = ParametricRegion((theta, pi), (2*sin(phi)*cos(theta), 2*sin(phi)*sin(theta), 2*cos(phi)),\
                            {theta: (0, 2*pi), phi: (0, pi/2)})
>>> ParametricIntegral(C.z, semisphere)
8*pi

I initially thought to make it a subclass of Integral as the ParametricIntegral is a kind of integral. But there was no reuse of any code from Integral in the ParametricIntegral so decided against it.
A rough sketch of the algorithm to calculate integral is described below:

1. Replace the base scalars in the field with their definition in terms of parameters and obtain the parametric representation of the field.
2. Form the position vector of the region using definition tuple and base vectors determined from the field.
3. Depending on the type of region, calculate the derivative of the position vector, or find the normal vector or calculate dV using Jacobian.
4. Calculate the integrand using dot product or multiplication with the parametric field.
5. Use the integrate function to calculate the integral.
6. If the integrate function can evaluate the integral, return it otherwise return an object of the ParametricRegion class.

We also had discussion on whether swapping the upper and lower limit has any affect on the result of a vector integral. For multiple integrals, the sign of the result changes when the upper and lower bound of a parameter are interchanged. I do not think we came to any conclusion. But this won’t matter for integrals over parametric regions as the bounds are directly defined by the user.

Next week’s goal

I will start working on the implementation of the ParametricIntegral class. I am also trying to get more involved in SymPy outside of my GSoC project. I hope I can become a contributing member of the community.

Key highlights of this week’s work are:

• Adds cdir parameter to handle series expansions on branch cuts

  • Finally, after spending almost 2 weeks on this, we were able to merge the PR, adding a very important functionality of series expansions on the branch cuts to the codebase. Previously, either SymPy raised some error or the series expansion was computed incorrectly, when the value in the input was on the branch cut. But now, for most of the functions, the expansion produced is correct.

    Not only this, we added the cdir parameter to leadterm and as_leading_term functions as well. We even extended the functionality a bit to the limits module, so now, limits of values lying on the branch cuts of a function are also computed correctly in most cases.

    We are planning to extend this functionality to all the remaining special functions and wherever else possible to make the codebase even more robust.

With this blog it completes the awesome month of statistical learning and coding, and the official Phase 1 of the Google Summer of Code-2020.

Key highlights of this week’s work are:

• Fixed incorrect evaluation caused due to subfactorial in limit_seq expression

  • This was a minor bug fix. The functionality of rewriting the subfactorial term present in an expression into an equivalent term expressed in the form of factorial or gamma was added which helped resolve the issue.
    
    

• Adds cdir parameter to handle series expansions on branch cuts

  • Currently, many functions in the codebase are unable to produce correct series expansions on branch cuts. As a result, the limit evaluation takes place incorrectly for these functions when the limiting value lies on the branch cuts.

    Thus, we have decided to come up with a parameter named cdir which stands for complex direction and it indicates the direction from which the series expansion is required, thus helping us to produce the correct series expansion. Special care needs to be taken while handling series expansions on the branch points.

    Once we are finished with this work, it will be a major enhancement to the limit evaluation and series expansion capabilities of SymPy.

This marks the end of Phase-1 of the program. I learnt a lot during this one month and gained many important things from my mentors.

The first week of GSoC has been completed. My goal for this week was to add ParametricRegion class. Many common regions have well known parametric representation. Calculation of Integrals on parametric regions is a common problem of vector calculus.

The PR for adding the ParametricRegion class is #19472.

ParametricRegion

An object of ParametricRegion class represents a region in space defined in terms of parameters. If a user wants to perform integration on a region, they have to create a ParametricRegion object. This object can then be passed to other classes to perform integration.

The implementation part was easy. The difficulty was in deciding the API. I spent much of the week discussing the API, But it was worth it. The ParametricRegion class will most likely be used by many users so it is important for it to be simple and intuitive. I think I should have first completed writing test cases and examples.

The final API of ParametricRegion class:

ParametricRegion(parameters_or_coordsys, definition, limits=None)

Some Examples:

p = ParametricRegion(t, (t, t**3), limits={t: (1, 2)})
halfdisc = ParametricRegion((r, theta), (r*cos(theta), r* sin(theta)), {r: (-2, 2), theta: (0, pi)})
cylinder = ParametricRegion((r, theta, z), (cos(theta), r*sin(theta), C.z), {theta: (0, 2*pi), z: (0, 4)})

parameters_or_coordsys

This argument specifies the parameters of the parametric region. When there are more than one parameter, the user has to pass them as tuple. When a CoordSys3d object is passed, its base scalars are used as parameters.

definition

definiton tuple maps the base scalars to thier parametric representation. It is not necessary for evey base scalar to have a parametric definition.

CoordSys3D

A parametric representation is just defining base scalars in terms of some parameters. If the base scalars are not knowm, the region cannot be completely specified. My intial approach was to include an argument to specify the coordinate system.

Passing a CoordSys3D object can be non intuitive for users. In most cases, the base scalars of the parametric region are the same as that of vector/scalar field. We can avoid passing the CoordSys3D object if we assume that the base scalars of parametric region field are same.

p = ParametricRegion((r, theta), (r*cos(theta), r*sin(theta)), limits={r: (0,1), theta: (0, pi)})
Integral(C.x**2*C.y, p)
# C.x = r*cos(theta),  C.y = r*sin(theta), C.z = C.z
Integral(R.x*R.y*R.z, p)
# R.x = r*cos(theta),  R.y = r*sin(theta), R.z = R.z

There can be a situation where SymPy cannot determine the coordinate system of the field. In such situations, we can raise a ValueError. For example:

Integral(R.x*C.z, p)

limits

Most parametric region have bounds on the parameters. Note that it is not necessary for every parameter to have an upper and lower bound.

There can be many methods for a user to define bounds of parametric region. We decied to use a dictionary which we named limits. The keys of the dictionary are parameters and the values are tuples (lower bound, upper bound). Another approach is to use a nested bound tuple. Every subtuple will represent the bounds of a parameter.

Next week’s goal

My next week’s task is to get started with ParametricIntegral class. This class will represent integral of a scalar/vector field on a parametric surface. I will first write the unit tests and examples.